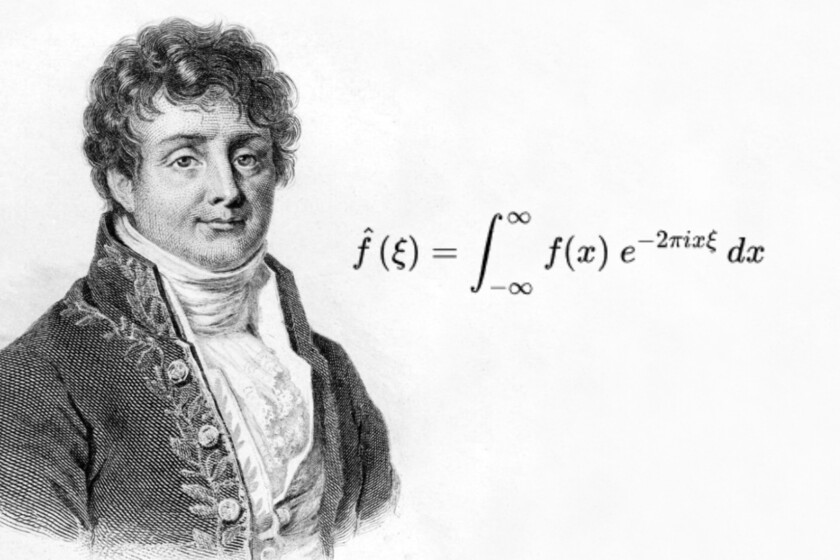The Fourier transform It is a fundamental mathematical operation for some disciplines such as telecommunications or physics. Without it, modern telecommunications would not exist, not only the Internet or mobile telephony, but also conventional telephony, which could not have evolved beyond a form of local communication and long distance calls would not have existed.
Although this mathematical operation owes its name to the mathematician Joseph Fourier, the truth is that many have contributed to its invention, including Euler, Bernoulli, Lagrange and Gauss. Fourier played an essential role, inventing the Fourier series, where a periodic function could be decomposed into the sum of trigonometric functions. The Fourier transform generalizes this concept.

The problem with this transform is that the math behind it is pretty advanced. You just have to take a look at the mathematical expression to visualize everything behind it. I’m going to put it here but I also anticipate that throughout this article we will see a simple explanation, both of the concept and of the mathematics behind it:

The Fourier transform, applications
Without going into evaluating the mathematics behind it, what the Fourier transform allows is convert any mathematical function to another domain, called the frequency domain. This makes it easy to treat and analyze the functions in an alternative way. As it is very generic, we are going to give an example.
A sound engineer may have a very noisy audio recording, for example because there was a beep in the environment. These noises can often be eliminated, but to do this it would be necessary to separate the part of the sound desired and the part to be eliminated. This separation is often impossible by conventional methods, since the signal is already added, and without knowing one of the parties it is impossible to eliminate the other.

However, with the Fourier transform, the signal can be seen in the frequency domain, that is, by decomposing the signal into the different frequencies that make it up (bass and treble sounds). Seeing the signal in this domain it is possible that the noise, which may have only some frequency components, is clearly separated, and therefore can be filtered, and return back to the temporal domain, thus having a signal clean of noise.
Something similar happens in telecommunications. Signals can be transmitted in the air through electromagnetic waves by separating them into different frequencies. This makes it possible to use the entire radio spectrum to transmit signals and thus be able to have radio, television, mobile telephony and Wi-Fi signals in the air (for example) in a given environment but that each electronic device listens to what it needs. All electronic devices have elements that are able to choose the frequencies they need and this is thanks to the mathematical development of the Fourier transform.
The Fourier transform made easy
It is clear that the applications of the Fourier transform are multiple, but even so the mathematical expression is quite complicated. The Youtuber ‘3Blue1Brown’ has created an impressive 20 minute video, in which what the transform means is explained graphically. But it does not remain only in what was said previously, but it goes so far as to explain in a very simple way what the apparently so complicated integral that we saw at the beginning means.
They are 20 very intense and interesting minutes that allow to visualize in a graphical way what the Fourier transform means and how it is possible to separate the frequency components of a function through it. It is like the magic of separating the colors of a mixture. You can see it below:
Basically what the video explains is the following: first, that the functions (which can be physical quantities such as sound waves) can be decomposed into sums of trigonometric functions (sines and cosines). The problem is that separating them is not easy. The example he gives is really good: if you mix two paints you get a new color, but from this mixture it is impossible to obtain the original colors.

The next thing he explains is a graphical way of representing the functions in an xy plane, so that we can see in the following steps what the Fourier transform is. And it is that the Fourier transform is find the center of mass of this xy representation.

The key is that the xy representation can be done in many ways (more or less winding the function) but when done at a rate similar to the fundamental frequency that the function contains, this center of mass is shifted, giving a maximum in the frequency representation. Explaining it in words is difficult, but the clarity of the video is astonishing.

Finally, the video is able to relate this graphical representation of compacting a function in an xy plane with the formula discussed at the beginning that represents the Fourier transform.


The video is very worthwhile and even people who have worked with it have seen the light and understand much better what this expression means thanks to it. I hope it is as clear to you as it is to so many others.